Dynamical Systems

For a class in computational physics that I took as an undergrad at UC Santa Cruz, I made an n-body simulation in Python. Given that the project is coded in Python, it runs rather slowly but allowed me to explore the stability of a planet around a binary star system, and was useful later in my graduate class on dynamical systems. The below figure illustrates how a slight variation in the planet's starting position can impact the stability of it's orbit.

For my undergraduate class, I further explored how the distance of the planet from the binary impacted orbit stability, but that is less relevant for the discussion of phase spaces.

During my graduate coursework at UC Santa Cruz I took a course in dynamical systems where I was assigned a project on phase space reconstruction. Takens (1981) outlines a method for determining whether or not a set of data can be attributed to a strange attractor. By time sampling the data, one can create a phase space diagram that, for systems governed by a strange attractor, forms a distinctive torus like shape. With proper selection of the number of dimensions and time sampling interval, this method works even for noisy systems.

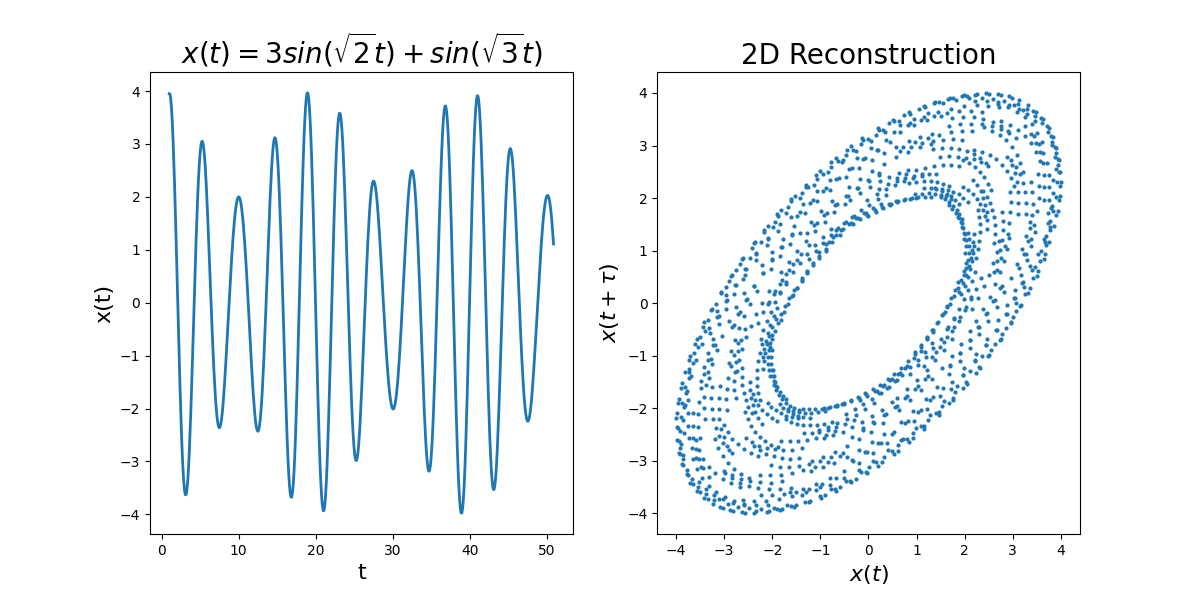
The below figure demonstrates the Takens theory of phase space reconstruction for a non-chaotic system. The right panel depicts time-delayed samples of the equation plotted at left. We can see a structure form and, under Takens' theory, we can understand the open donut shape to indicate the presence of an attractor.

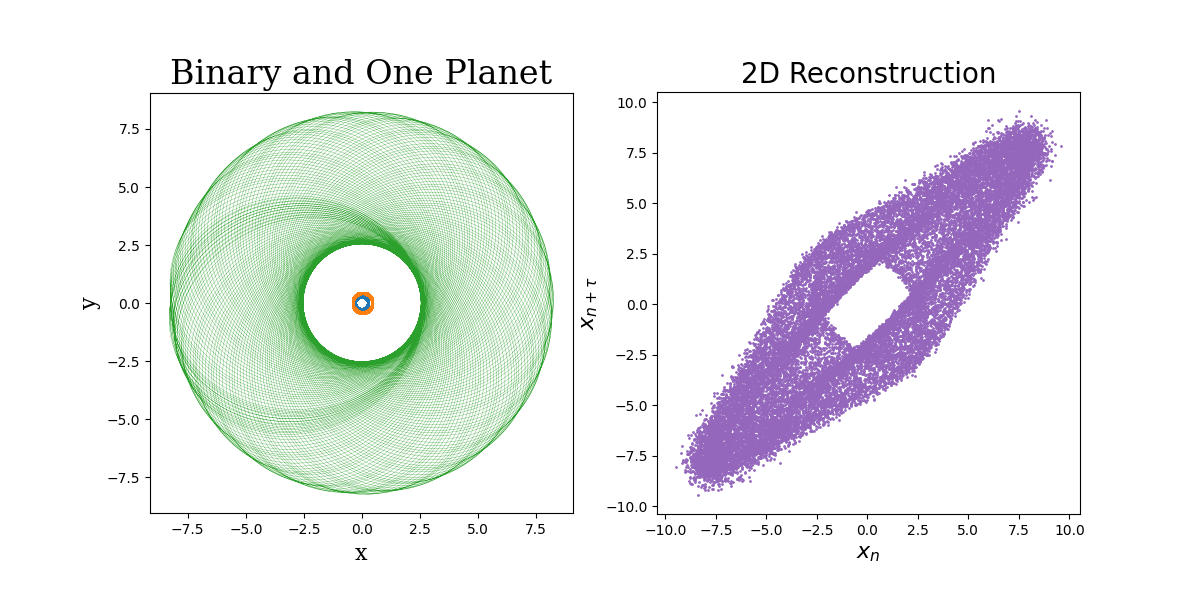
What's remarkable about the Takens theory is that is also works for chaotic and noisy systems where it may be less obvious that an attractor is present. To demonstrate this, I took positions of the planet in my n-body simulation and applied Gaussian noise to them. The below figure illustates the 3 body system, one planet and two stars, in the left panel and the phase space reconstruction in the right panel. While the structure of the reconstruction is not as clean and open as the simpler system above, the clear structure and still somewhat present donut aspect indicate an attractor governs the system. Of course, given that this is a gravity simulation, we know that an attractor is indeed present.